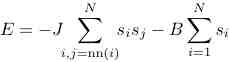 ,
,
Introduction
The simplest, nontrivial model that has a phase transition is the Ising model, one of most important models in statistical mechanics. The model consists of spins located on a lattice such that each spin can take on one of two values designated as up and down or ±1. The interaction energy between two neighboring spins is -J if the two spins are in the same state and +J if they are in opposite states. The Ising model undergoes a phase transition between an ordered and a disordered phase in two dimensions or more. We will consider the Ising model in the context of magnetism, but many other systems can be understood in terms of the Ising model.
The model was proposed by Wilhelm Lenz (1888–1957) in 1920 and was solved exactly for the one-dimensional case by his student Ernst Ising in 1925. The one-dimensional case does not have a phase transition. Lars Onsager (1903–1976) solved the Ising model exactly in 1944 for two dimensions in the absence of an external magnetic field and showed that there was a phase transition in two dimensions. No exact solution is available in two dimensions in an arbitrary magnetic field and in three dimensions. Hence, simulations of the Ising model are essential.
The total energy can be expressed in the form
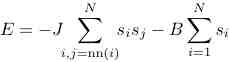 ,
,
where si =±1 and J is the exchange constant. We will refer to s as the spin.
Simulations of the Ising model are available for one dimension, square lattice (J > 0), square lattice (J < 0), and hexagonal lattice (J < 0). Also available are numerical solutions of mean-field theory, the direct simulation of the density of states, the direct simulation of the partition function, and a simulation of hysteresis.
References
Each year many hundreds of papers are published that apply the Ising model to problems in such diverse fields as neural networks, protein folding, biological membranes, and social behavior.
Updated 5 March 2009.