The Ising antiferromagnet on a hexagonal lattice

Introduction

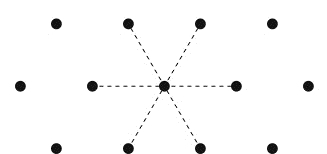
Before you consider the Ising antiferromagnet on a hexagonal lattice, you should understand the qualitative behavior of the Ising ferromagnet and antiferromagnet on the square lattice. Do you expect the physical properties of the hexagonal Ising model with J = + 1 or J = -1 to be qualitatively different from the properties of the Ising model on a square (or rectangular) lattice? The following figure illustrates the nature of the hexagonal lattice.

Note that the coordination number, the number of nearest neighbors, is six. What is the coordination number of the square lattice?

    Recall that for J > 0, the energy is minimized when neighboring spins are parallel. If J < 0, the energy is minimized when neighboring spins are antiparallel. As we will see, changing the number of nearest neighbors changes everything. Look at the figure below. The spin at the site denoted by a question mark is frustrated. If it is antiparallel to one neighbor, it must be parallel to the other neighbor. On a hexagonal lattice it is impossible for all neighbors to have opposite spins. The system is frustrated because it cannot achieve a state where all the spins have neighbors that are antiparallel. (This type of frustration is geometrical in nature in contrast to the frustration associated with a spin glass in which the exchange constant J is randomly chosen to be ± 1.)

Problems

1. Run the simulation at various temperatures and qualitatively describe the configurations. The program plots the magnetization and the energy as a function of time (number of Monte Carlo updates per spin) on the same graph. Which curve is which?
2. We know the Ising model on a square lattice with J > 0 or J < 0 has a phase transition. Does the Ising model on a hexagonal lattice with J < 0 have a phase transition?
3. Consider a small lattice, for example, L = 4, and construct several ground states to convince yourself that there are multiple ground states. The connection between frustration and the number of ground states is a subject of current research interest.

Updated 4 March 2009.