Number of states of a particle in a box: Finite size effects

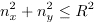
Introduction

As discussed in Pathria and many other texts, the number of states for one particle in a two-dimensional box is given by the values of n_x and n_y that satisfy the condition

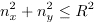
where the quantum numbers n_x and n_y are nonzero positive integers. R is related to the energy of the system by

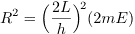
where L is the linear dimension of the box, m is the mass of the particle, and h is Planck's constant.

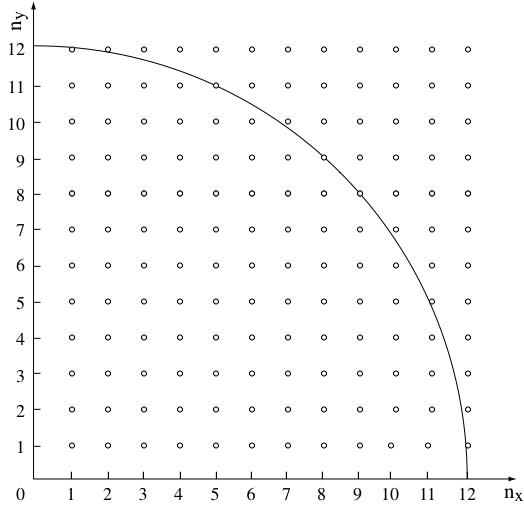
     In the semiclassical limit where E is large, the number of states with energy less than or equal to E is given by the area of the positive quadrant of a circle of radius r:

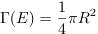
However, the number of states for finite values of R (and E) is different than this asymptotic expression (see the figure).

    The program shows the asymptotic expression and the actual number of states. The latter is given by

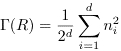
where d is the spatial dimension of the box and

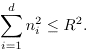
Problems

1. Derive the various formulas that have been discussed.
2. Does the asymptotic expression for Γ under or over estimate the actual number of states? (The program works for dimension d = 1,2, and 3.)
3. What is the minimum value of R such that the difference between the actual and the asymptotic expression for the number of states is less than one percent?

Reference

• R. K. Pathria, Statistical Mechanics, second edition, Butterworth-Heinemann (1996), pp. 18–19.

Java Classes

• NumOfStatesApp

Updated 4 March 2009.