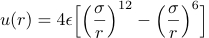Lennard-Jones system of particles

Introduction

The exact form of the interparticle potential u(r) for electrically neutral molecules and atoms has to be determined by a first principles quantum mechanical calculation. Such a calculation is very difficult, and for many purposes it is sufficient to choose a simple phenomenological form for u(r). The most important features of u(r) are a strong repulsion for small r and a weak attraction at large r. The most common phenomenological form of u(r) is the Lennard-Jones or 6-12 potential proposed by John Edward Lennard-Jones in 1924:

,

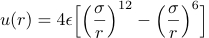The values of σ and ε for argon are σ = 3.4 × 10^-10 m and ε = 1.65 × 10^-21 J.

    The existence of many calculations and simulation results for the Lennard-Jones potential encourages us to consider it even though there are more accurate forms of the interparticle potential for real gas and liquids.

    It is possible to simulate a system of Lennard-Jones particles using either molecular dynamics or Monte Carlo methods.