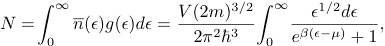Thermodynamics of the Ideal Fermi gas

Introduction

To find the chemical potential μ of an ideal Fermi gas for T > 0 , we need to find the value of μ that yields the desired number of particles. We have

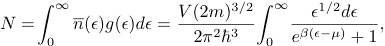(1)

where g(ε) is the density of states for a system of electrons:

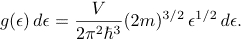(2)

Our goal is to find the value of μ that gives the desired density ρ = N/V. Because the integral in Eq. (1) cannot be done analytically except at low temperatures, we will use numerical methods to evaluate it.

    It is convenient to let ε = xε_F, μ = μ*ε, and T* = kT/ε_F, where ε_F is the usual Fermi energy.

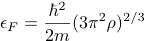(3)

Then we can rewrite the expression for N as

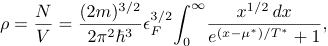(4)

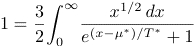(5)

    Similarly, the mean energy E can be expressed as

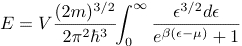(6)

If we make the same substitutions as before, we find

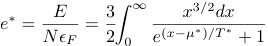(7)

The program evaluates the integrals for μ* and e* numerically.

Problems

1. Start with T* = 0.2 and find μ* such that the first integral is satisfied. Click on the Accept Parameters button when the value of μ* satisfies the condition that the integral on the left-hand side of Eq. (5) is approximately 1.0. Does μ* initially increase or decrease as T* is increased from zero? What is the sign of μ* for T* >> 1?
2. At what value of T* is μ* ≅ 0?
3. Each time you compute a value of μ* for a given value of T*, the program plots the corresponding value of e* by evaluating the integral in Eq. (7). How does e* vary with T* for T* << 1 (T << T_F)? Use your results for the mean energy to determine the temperature dependence of the specific heat.

References

The properties of the ideal Fermi gas are discussed in almost all texts on statistical mechanics.

Updated 28 December 2009.