Simple thermal interaction: Einstein solid
Consider a simple system commonly known as an Einstein or harmonic solid. The energy of each particle in an Einstein solid is restricted to the positive integers. That is, each particle may have energy 0, 1, 2, … The particles do not interact.
One advantage of the Einstein solid is that it is easy to calculate the number of microstates Ω(E,N) for a energy E and given number of particles N.
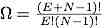 .
.
Consider two Einstein solids A and B that can exchange energy with one another, but are isolated from their surroundings. That is, the two systems are surrounded by insulating, rigid, and
impermeable outer walls and are separated from each other by a conducting,
rigid, and impermeable wall. The program counts the number
of ways that the energy can be distributed between the two systems for given values of NA, the number of
oscillators in system A, and NB, the number in system B.
The total number of microstates Ω(EA, EA) accessible to the composite system with subsystems A and B with energy EA and EB (and fixed number of particles NA and NB) is
Ω(EA, EB) = ΩA(EA)ΩB(EB).
The total energy E = EA + EB is fixed. Because the composite system is isolated, its accessible
microstates are equally probable. Hence, the probability PA(EA) that subsystem A has energy EA is
PA(EA) = ΩA(EA)ΩB(E - EA)/Ω.
The output of the program is the mean energy of system A and the probability P(EA) that system A
has energy EA.
- Suppose that NA = 2, NB = 2 and initially EA = 5 and EB = 1. What is the initial number of microstates for the composite system? The internal constraint is then removed so that the two subsystems can exchange energy. Determine
the probability
P(EA) that system
A has energy
EA, and the
most probable energy of system A. What is the total number of microstates after the internal constraint has been removed? Discuss the qualitative dependence of
P(EA) on the energy EA. The corresponding numerical values can be obtained by choosing DataTable from the Views menu. Use this data to calculate
the mean and variance of the energy of each subsystem.
- Answer the same questions as in Problem 1 with NA = 20, NB = 20, EA = 100, and EB = 20.
- Answer the same questions as in Problem 1 with NA = 20, NB = 40, EA = 100, and EB = 20.
- If the two subsystems have equal numbers of particles, it is reasonable to conclude that the "hotter" system has higher energy. What is the probability that energy goes from the hotter to the colder system after the internal constraint has been removed?
- Consider
successively larger systems until you have satisfied yourself that
you understand the qualitative behavior of the various quantities. Discuss your general qualitative conclusions.
- Consider a special subsystem with only one particle, NA = 1. Suppose that NB = 5, EA = 0, and EB = 12. If we assume that the subsystem A can exchange with the much larger system B, what is the probability that system A has energy EA? What is the probability that system A is in a particular microstate with energy n where n is an integer? The probability in this case is called the Boltzmann probability. Why is the form of this probability different than the probability that you found in the other problems?
- Harvey Gould and Jan Tobochnik, Statistical and Thermal Physics, Chapter 4.
- Thomas A. Moore and Daniel V. Schroeder, "A different
approach to introducing statistical mechanics," Am. J. Phys. 65, 26–36 (1997).
- Daniel V. Schroeder, An
Introduction to Thermal Physics, Addison-Wesley (1999).
- EinsteinSolid
- EinsteinSolidApp
Updated 26 December 2009.
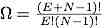 .
.
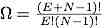 .
.