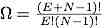Simple particle exchange: Einstein solid

Introduction

Consider a simple system known as the Einstein or harmonic solid. The energy of each particle in an Einstein solid is restricted to the positive integers. That is, each particle may have energy 0, 1, 2, … The particles do not interact.

    One advantage of the Einstein solid is that it is easy to calculate the number of microstates Ω(E,N) for a given number of particles N and energy E.

.

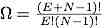    Consider two Einstein solids A and B that allow particles to move from one solid to the other, but not energy. That is, the two systems are surrounded by insulating, rigid, and impermeable outer walls and are separated from each other by a wall that allows particles to move through it, but no energy. This constraint is unphysical, but it will be useful conceptually for understanding the chemical potential. The program counts the number of ways that the particles can be distributed between the two systems. N_A is the number of oscillators in system A and N_B is the number in system B.

    The total number of microstates Ω(E_A,E_A) accessible to the composite system with subsystems A and N with fixed energy E_A and E_B and number of particles N_A and N_B is

Ω(E_A, E_B) = Ω_A(E_A)Ω_B(E_B).

Because the composite system is isolated, its accessible microstates are equally probable. Hence, the probability P_A(N_A) that subsystem A has particle number N_A is

P_A(N_A) = Ω_A(N_A)Ω_B(N - N_A)/Ω.

    The output of the program is a plot of P_A(N_A) and the corresponding table of data.

Problems

1. Suppose that E_A = 8, E_B = 5 and N = 10. View the Data Table. For what value of N_A does the total system have the maximum number of microstates? The chemical potential over kT is computed as the negative numerical derivative of the ln Ω_i with respect to N_i. How do the chemical potentials compare when the number of states is a maximum?
2. We will assume that equilibrium is the state with the maximum number of microstates. If a system starts out with unequal chemical potential, do the particles move from the solid with higher chemical potential to that with lower chemical potential or vice versa?
3. Repeat for other values of E_A, E_B and N, and verify that the same qualitative behavior occurs. Under what conditions does P_A(N_A) become sharply peaked?

Reference

• Harvey Gould and Jan Tobochnik, Statistical and Thermal Physics, Chapter 7.

Java Classes

• EinsteinSolidChemicalPotentialApp

Updated 14 April 2010.